Notification
You need to select an answer first.
Knowing Formal Logic is necessary for taking the LSAT. This content may be alien to you, so we start slowly and move through the topics in a simple and intuitive fashion.
The most basic logic concept is necessary vs. sufficient.
“P is sufficient for Q” means:
The truth of P is enough for the truth of Q
P cannot be true without Q being true
If P is true, then Q is true
(informally) P is all you need for Q
“P is necessary for Q” means:
Q cannot be true without P being true
Q is not true unless P is true
If Q is true, then P is true
Q is true only if P is true
(informally) P is needed for Q, can’t have Q without P
Register for a free demo class and a free LSAT from Kaplan.
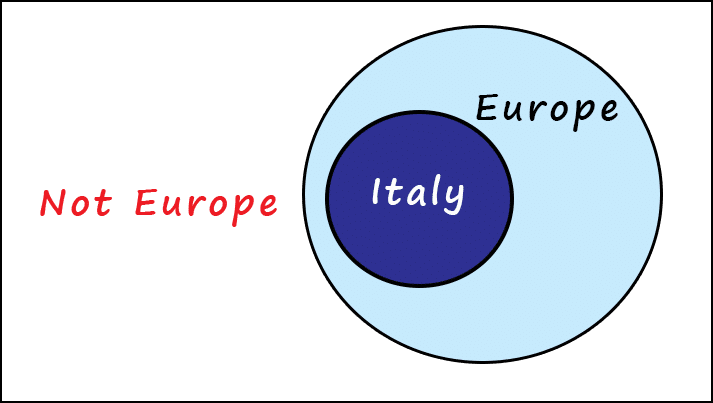
Being in Italy is sufficient for being in Europe.
Being in Europe is necessary for being in Italy.
Being in Italy is not necessary for being in Europe (one can still be in Europe outside Italy, in Greece for example).
Being in Europe is not sufficient for being in Italy (for the same reason as above).
Kaplan offers six classes a week. Register for a free demo class.
Next LSAT: Sep 08/ Sep 09
Identify whether each of the following statements presents a necessary condition, a sufficient condition, both, or neither.
Do not make any extraordinary assumptions when answering these questions.
(Remember the notion of background assumptions from the above video at 1:52)
Watering a plant is _______________ for it to grow.
Necessary but not Sufficient
Watering a plant is a necessary but not sufficient condition for it to grow. It is necessary because water is required for plants to grow. However, it is not sufficient because plants also need other things for growth, such as sunlight and proper soil.
Finishing college is _______________ for one to be rich.
Neither Necessary nor Sufficient
Finishing college is neither necessary nor sufficient for being rich. Some people did not finish college but still became rich. Moreover, finishing college does not guarantee that a person will become rich.
Knowing the correct formula is _______________ for finding the volume of an object in a math exam.
Necessary but not Sufficient
Knowing the correct formula is a necessary condition for solving the volume of an object in a math exam because using an incorrect formula will lead you to a wrong answer. However, it is not a sufficient condition because knowing the formula is not enough. You still have to do the calculation correctly to get the correct volume.
Given that the passing score for the midterm science exam is 70%, getting a score of 70% or higher in the exam is _______________ for passing it.
Necessary and Sufficient
It is both necessary and sufficient that one gets a score of 70% or higher in the midterm science exam in order to pass it. It is a necessary condition because the passing score for the midterm science exam is precisely 70%, so getting 70% or higher is required for you to pass it. Moreover, it is also a sufficient condition because getting a passing score automatically means that you pass the exam.
Living in Hong Kong is _______________ for living in Asia.
Sufficient but not Necessary
Living in Hong Kong is a sufficient but not necessary condition for living in Asia. If one lives in Hong Kong, then it automatically means that they also live in Asia, since Hong Kong is in Asia. However, it is not necessary because one can live in other countries in Asia other than Hong Kong.
Every working day, John takes the metro line D at 8:30, which takes him to work in 35 minutes. His work regularly starts at 9:30. However, tomorrow his shift starts at 9:00. Therefore, it is _____________________ condition that he takes the same line at least five minutes earlier than usual for not being late to his work tomorrow.
Both Necessary and Sufficient
It takes John 35 min to get to work. It is enough to take the metro 5 min earlier than the usual 8:30 to arrive at 9:00. Therefore, the condition is sufficient. If he fails to depart at least 5 min earlier, he will have less than 35 min to travel and will be late. He needs to depart at least 5 min earlier. Therefore, the condition is necessary. (Note that taking the metro exactly 5 min earlier is not necessary for being on time, because he can depart 15 min earlier and not be late; however, our condition is not to depart exactly, but at least 5 min earlier, which is necessary for arriving at 9:00.)
Therefore, the condition is both sufficient and necessary.
This is an adaptive drill: The questions will get harder or easier depending on your performance. You can't go backwards or change prior answers.
Complete: 0 / 7 correct
Next LSAT: Sep 08/ Sep 09