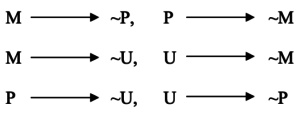For grouping games, you may want to create a second list of the groups into which you will be dividing the elements. In this case, the groups are the three buildings: Genius Hall, Intellectual Center, or Brainy Building.
Groups: Genius, Intellectual, Brainy (g, i, and b)
Notice that we represent the group names with lower case letters, rather than the capital letters we used to represent the students. It’s always a good idea to make your abbreviations for the roster of elements and the abbreviations for the groups look different so you don’t run the risk of mixing them up during the process of solving the game.
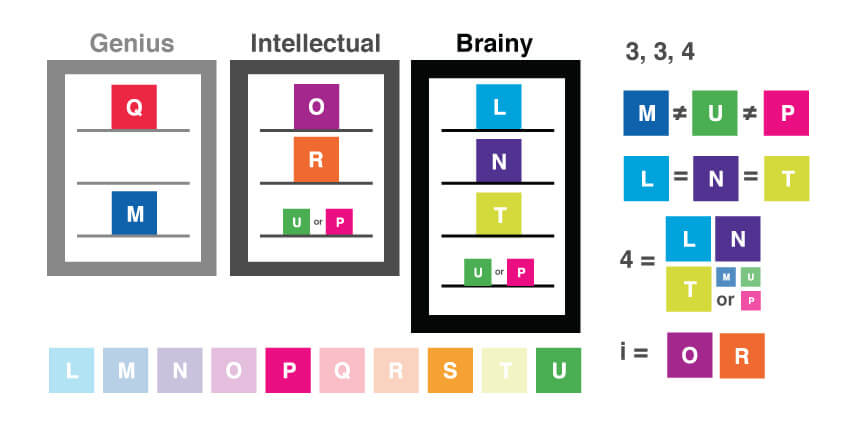
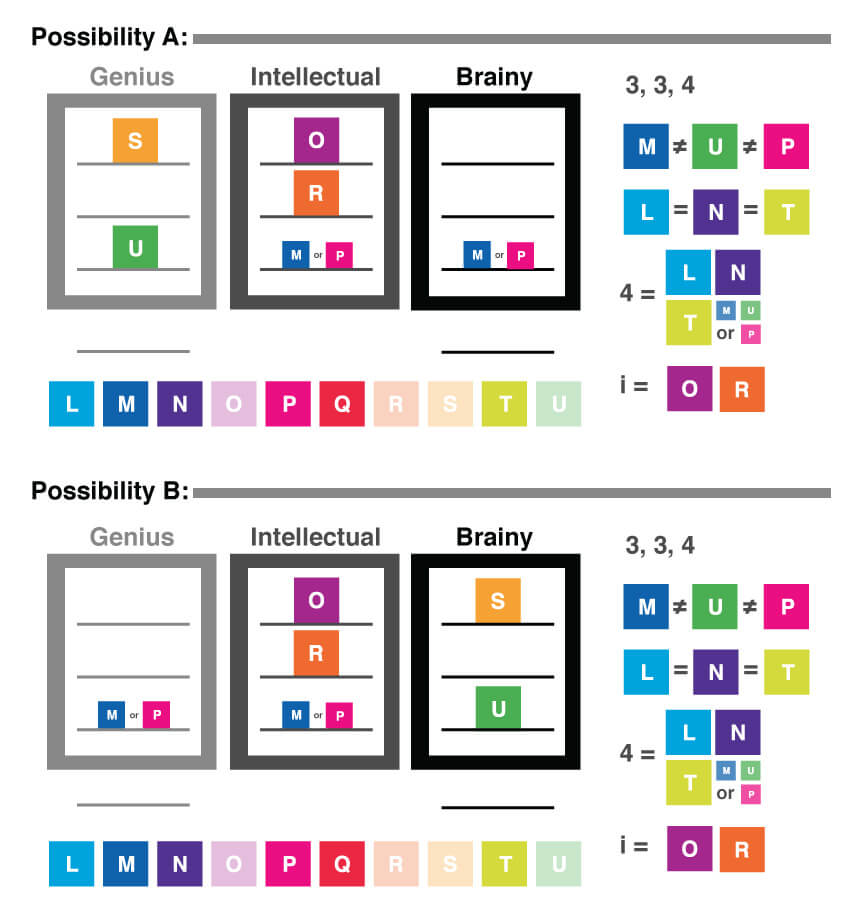
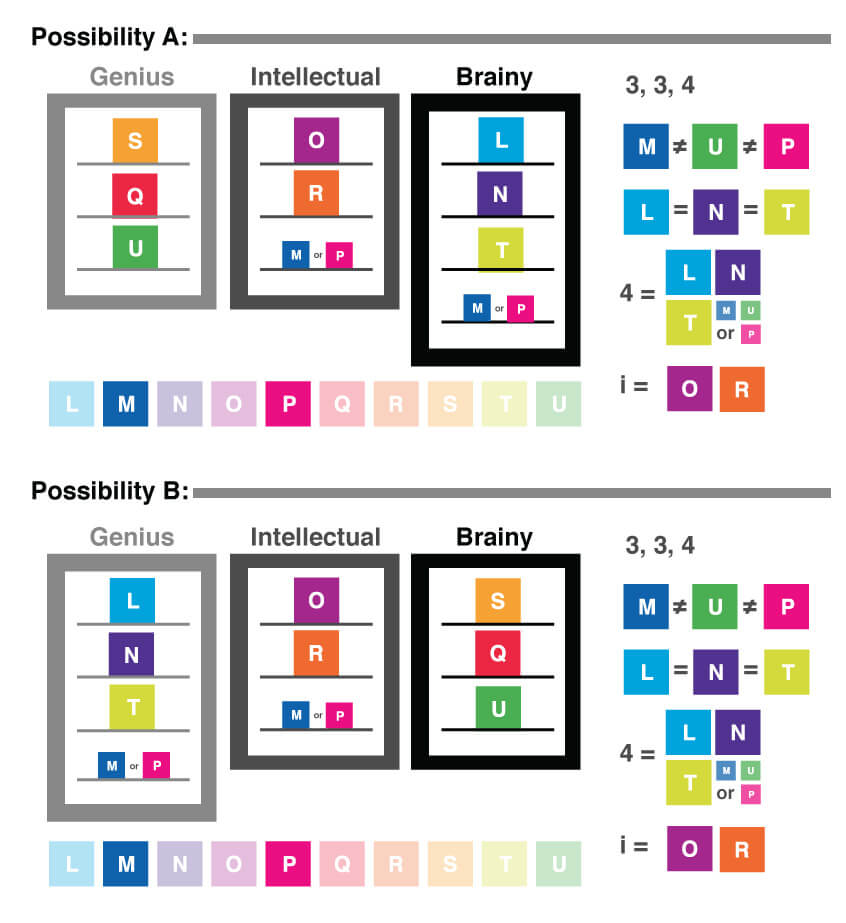
Okay, according to our game-solving strategy, our next step is to symbolize the conditions. In this case, one of the conditions is actually contained within the premise of the game: we are told that at least three students are assigned to each of the three dormitories. What additional information can we deduce from that statement? Well, if there are ten students, and at least three will be in each dorm, that would give us three students in three dorms, for a total of nine students. Since we have ten students, not nine, we can conclude that one of the dormitories will have four students, and the other two will have three students each. We don’t know yet which of the three dormitories has four students, and which two have three, but for now, we can summarize this simply as 3-3-4.
The next condition (the first in the list of conditions following the premise) tells us that M, P, and U are all assigned to separate dormitories. This means that if M is in a dorm, then neither P nor U can be in that same dorm. (This applies to the others as well, that is, if P is in a dorm, then M and U are not in that dorm, etc.) We can use the same symbol we used earlier to indicate not (the “~” symbol) and represent this condition as:
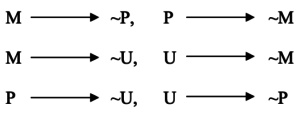
(Conditional Relationship Diagrams)
As you can see, that one sentence condition has given us a lot of information. We know that these three students are assigned to the three different dormitories. How else could we represent this condition symbolically? Rather than writing three lines, a shorter way might be to just use the ? symbol. In this case, we can use it to represent the fact that if one of the students is assigned to a dorm, the others cannot also be assigned to that dorm:
M ? U ? P
The next condition tells us that students L, N, and T are all assigned to the same dormitory. Using the opposite symbol from that which we used for the previous condition, we can represent this as:
L = N = T
Again, what other information can we deduce from this condition? Since we know that two of the dormitories will have three students and one will have four, we know that either only these three students will live in one dormitory, or one additional student could also be assigned to the same dormitory and that this dormitory would then be the one that has four students. Now, let’s think about the previous condition. We know that students M, U, and P all live in separate dorms (M ? U ? P). That means that one of them, though we don’t yet know which one, will be assigned to the same dorm as L, N, and T. Therefore, we can modify our condition to represent this new information:
4 = L, N, T and (M, U, or P)
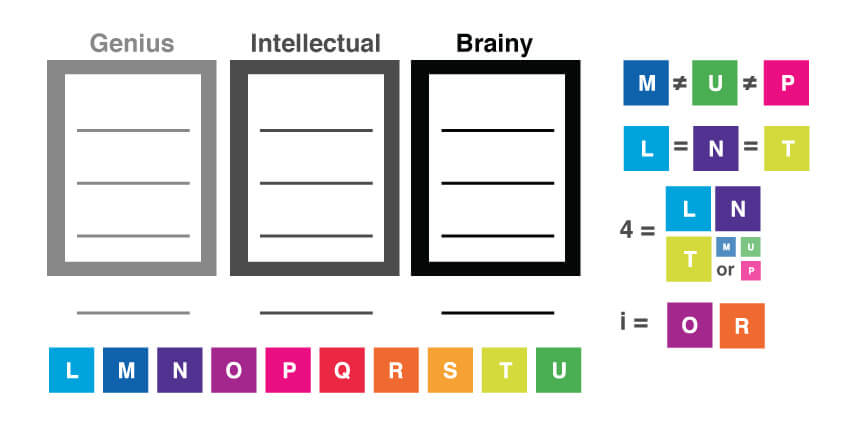
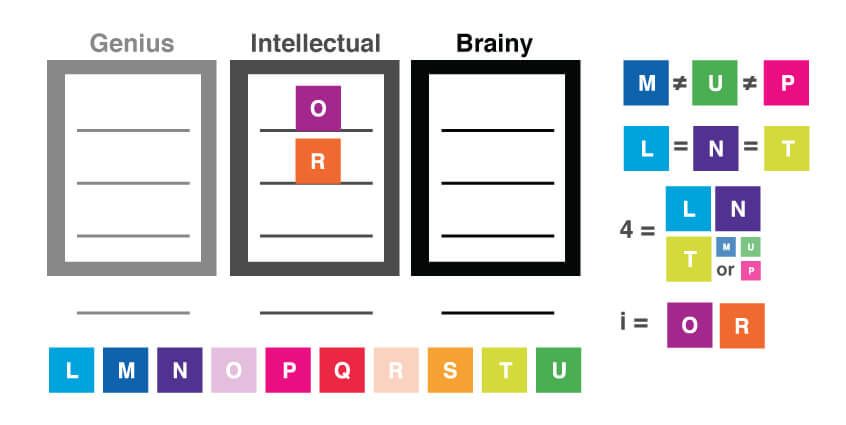
The third condition tells us that both O and R are assigned to Intellectual Center. We can represent this condition as:
i = O and R