Congratulations on finishing the Logic Games course.
Logic Games Strategies
SKIP A GAME?
The four LSAT games typically get progressively difficult. If you are a below average LSAT student, you should probably aim to just solve three of the games (the easier three). If one game is impossible and you are getting bogged down, fold and move on. Don’t get caught up in the Sunk Cost Fallacy, which is when you continue in a pointless task simply because you have invested so much into it.
Sample Questions
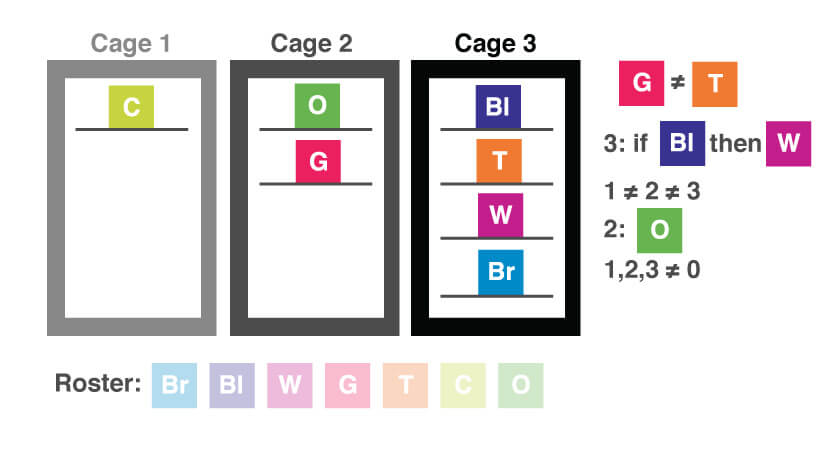
In the front window of Peter’s Pet Palace, there are three cages — cage one, cage two, and cage three — that contain a total of seven cats. Each cat is a different color: brown, black, white, gray, tabby, calico, or orange. The gray cat and the tabby cat are not in the same cage. The black cat is in cage three only if the white cat is also in cage three. Each cage contains a different number of cats. The orange cat is in cage 2. There is at least one cat in each cage.
GAME SETUP WALKTHROUGH
Okay, once we have read the premise, we can see that this is a grouping game. What are the groups? What are the elements we are asked to arrange into these groups? The groups are the three cages that contain the cats. The cats are the elements we need to arrange. We have seven cats of varying colors.
Our roster might look like this:
Roster: Br, Bl, W, G, T, C, O
Note that we had two colors starting with B, so we just used Br and Bl to help us differentiate between those two cats.
Groups: (cages) 1, 2, and 3
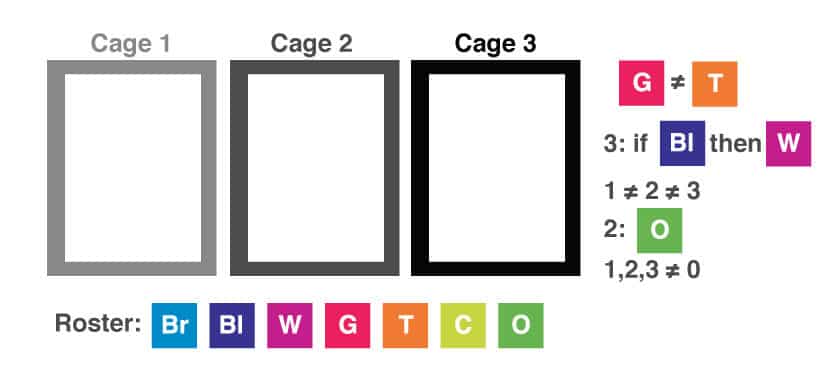
Next, let’s symbolize the conditions. The gray cat and the tabby cat are in different cages. This can be summarized as: If G, ^T or if T, ^G.
We can also write this as G ≠ T.
The second condition tells us that the black cat is in cage three only if the white cat is also in cage three. We can write this as: 3: if Bl, then W
The next condition tells us that each cage contains a different number of cats. This can be represented as 1 ≠ 2 ≠ 3
We are told that the orange cat is in cage 2. This is simply represented as: 2: O
Finally, we are told that there is at least one cat in each cage. We can write this as: 1, 2, 3 ≠ 0
What else does this statement tell us? Well, if there are three cages, each containing one cat, and we have seven cats all together, then the maximum possible number of cats in any one cage would be five. (Since one cat would be in each of the other cages.)
Let’s draw a diagram to help us think about the problem.
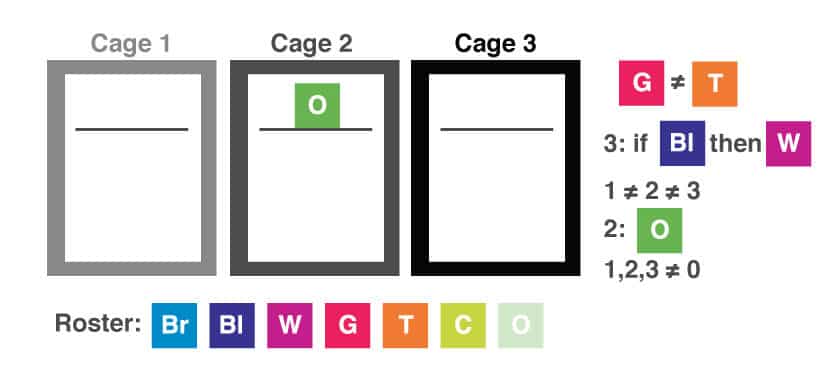
Is there any information that we can extract from the conditions and put onto the diagram? Let’s start with fixed conditions. We can put at least one line in each cage since we know there is at least one cat in each one. We can also place the orange cat (O) in cage 2.
Can we place with certainty any information from the other conditions? We could also include the statement about the cats that might be in cage 3 (3: if B, then W). Though since we don’t know yet where any cats (other than the orange one) are, let’s wait on this one until we’ve read the question.
Question One
If cage 1 contains only the brown cat, then which of the following may be true?
(A) Cage 2 contains only the orange, black, and calico cats.
(B) Cage 3 contains only the black, white, and calico cats.
(C) Cage 2 contains only the tabby, calico, gray, and orange cats.
(D) The black and white cats are the only two cats in cage 3.
(E) The gray cat is in the same cage as the white cat.
EXPLANATION
After reading the question, the first step is to determine whether there is any additional information provided by the question. In this case, we are told that cage 1 contains only the brown cat, so we can add that to our diagram. Next, we want to consider the original conditions and determine whether in combination with our new information, we can move anything else to our diagram. In this case, we know that there is a different number of cats in each cage. Since there is only one cat in cage 1, we know that there must be at least two in both cages 2 and 3. Since there are seven cats total, we also know that we need to place six cats into cages 2 and 3. It cannot be exactly three cats in each cage or that would violate the rule of there being a different number of cats in each cage. We can make a note of that at the bottom of groups 2 and 3.
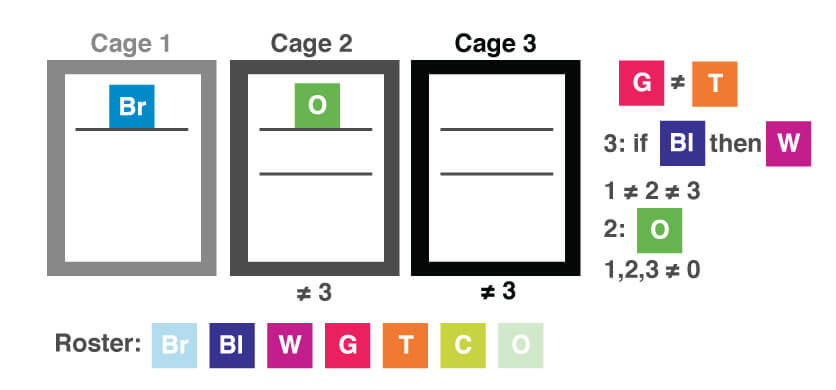
Now let’s work through the answer choices, keeping in mind that we are being asked for which arrangement may be true. Choices (A) and (B) cannot be correct since they place only three cats in either cage 2 or 3, and we just concluded that it is impossible to have only three cats in these cages since that would violate the 1 ≠ 2 ≠ 3 rule. Choice (C) does not violate the same rule, though when we look over our conditions, we see that it violates the G ≠ T rule, so we can eliminate this option. Choice (D) puts only the black and white cats in cage 3. We know that the black cat can only be in this cage if the white cat is present, which is the other part of this answer choice. What happens if we add these two cats into our diagram in cage 3? Keep in mind that only the brown one is in cage 1, we already have the orange one in cage 2, and we still need to fit the other three cats into a cage, and the only one available is cage 2.
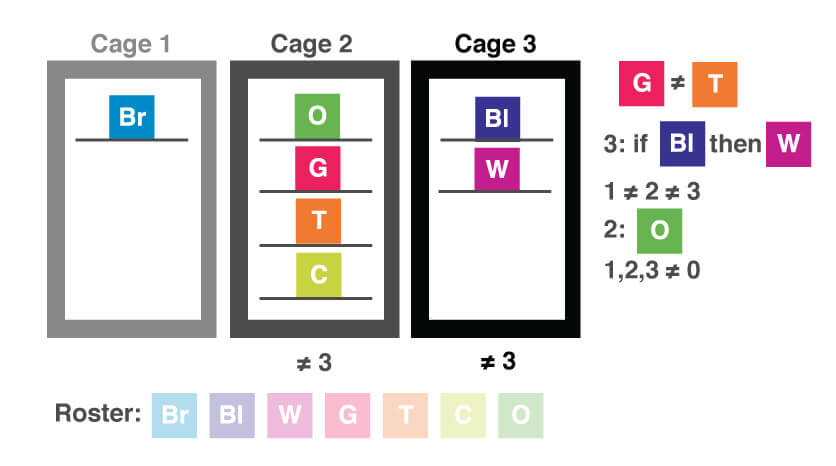
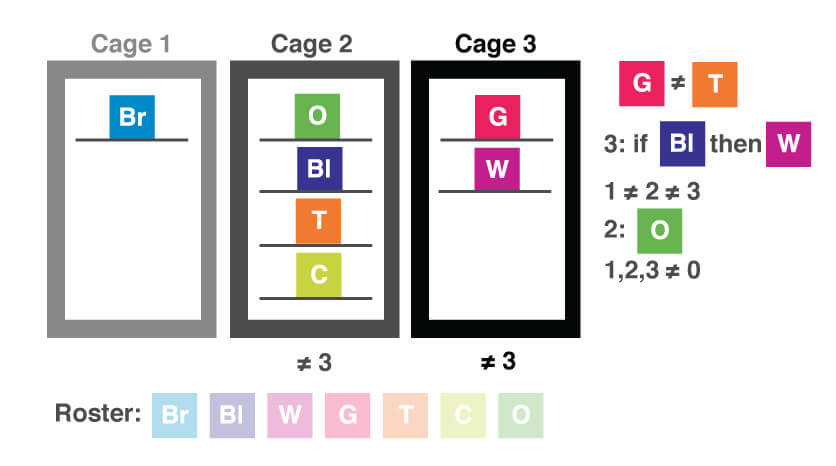
When we do this, we can see that this arrangement will violate the G ≠ T rule, so this is not a possibility. Choice (E) is the only one left, but let’s check it to make sure. The gray cat is in the same cage as the white one. Is this possible? Let’s try placing the two cats into cage 3. We know we need to have the tabby in a different cage from the gray cat, so we must put the tabby in cage 2. The other cats can be in either cage as long as we can figure out an arrangement that places a different number of cats in each cage. Here is one possibility, though there are several:
Next LSAT: Sep 08/ Sep 09
Question Two
If the black cat and the tabby are two of the cats in cage three, then which of the following must be false?
(A) The gray cat and the calico are the only two cats in cage one.
(B) The calico and the brown cat are also in cage three.
(C) There are two cats in cage two.
(D) Besides the black and tabby cats, there are two more cats in cage three.
(E) The orange cat and the gray cat are in the same cage.
EXPLANATION
After reading the question, let’s add the new information to our diagram. Remember, we will go back to our original diagram, not the one on which we added information specific to the last question.
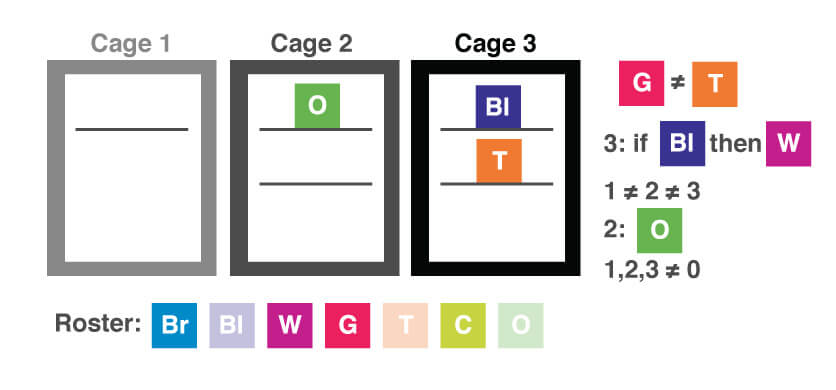
We know that if the black cat is in cage three, then the white cat must also be in cage three, so we can add that information to our diagram.
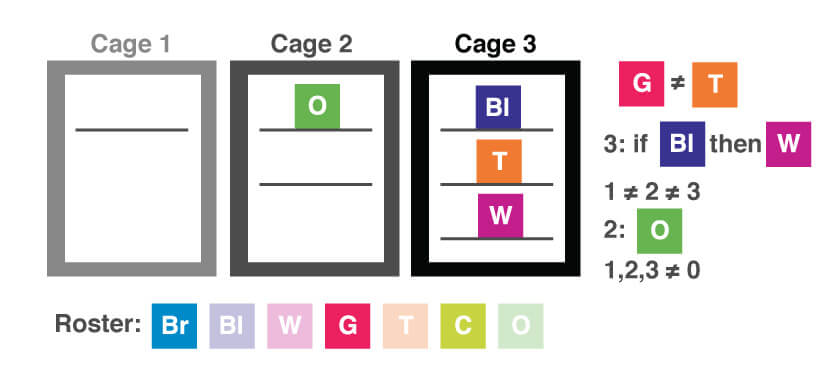
Now let’s work through the answer choices with the help of our diagram, keeping in mind that we are looking for the choice that must be false. Starting with choice (A), can we place the gray and calico cats in cage one? Well, if we have two cats there, we need to have five cats total in cages two and three. We already know where four of those are (the black, tabby, and white cats are in cage three, and the orange cat is in cage two), so we would just need to place the brown cat. Can we place the brown cat in cage two? No, that would put two cats in both cages one and two, violating the 1 ≠ 2 ≠ 3 rule. Can we put it in cage three? Yes, so this choice is acceptable. Choice (B) puts the calico and the brown cat in cage three. If we add these two cats to the three we have already placed in cage three, that would give us five cats there, leaving only two for cages 1 and 2, again violating the 1 ≠ 2 ≠ 3 rule. This choice must be false, which is what we are looking for. Let’s look at the other answer choices, though, just to convince ourselves. Choice (C) places two cats in cage two. That would be the orange cat plus one other. Can we still place the remaining cats and satisfy the other conditions? Yes, here is one such arrangement.
Choice (D) puts a total of four cats in cage four. Is this possible? Yes, the last example actually satisfies this condition, too. Choice (E) requires the orange and gray cats to be in the same cage, and we can easily see that this is a possible arrangement. Therefore, the one choice that must be false is choice (B).
Next LSAT: Sep 08/ Sep 09







