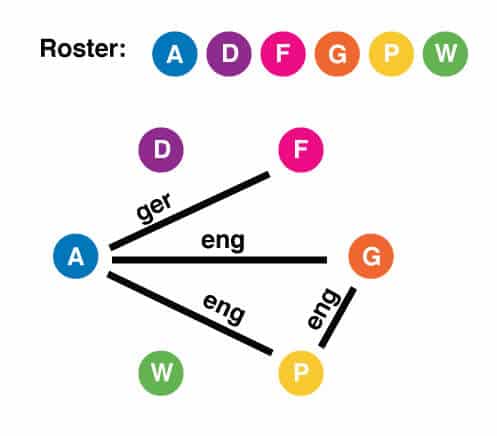
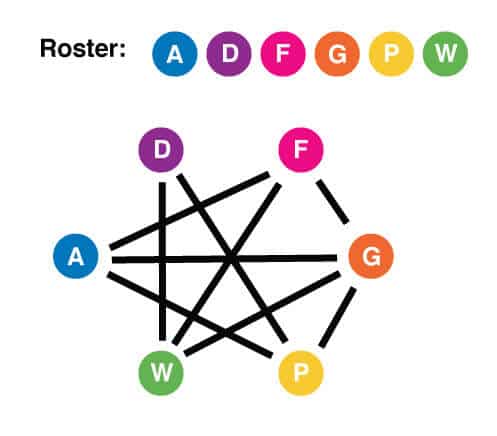
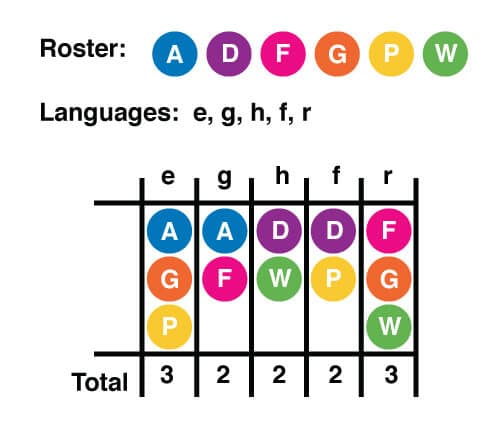
Now that we have the network diagram, let’s try some questions.
Question One
(1) If Mr. Das and Mr. Gaal wish to converse, which of the following represents a complete list of the people who could serve as an interpreter?
(A) Mr. Andrews only
(B) Ms. Petrucci only
(C) Ms. Win only
(D) Ms. Petrucci and Ms. Win only
(E) Mr. Andrews, Ms. Petrucci, and Ms. Win only
Solution
Mr. Das and Mr. Gaal do not share a language, that is, we have drawn no line connecting them. An interpreter would be someone who can speak the same language as Mr. Das and also speak the same language as Mr. Gaal. We are looking for an element that is connected to D and connected to G. Choice (A) is Mr. Andrews. A is connected to G, though not to D, so this cannot be the correct answer. Choice (B) is Ms. Petrucci. In our diagram, P is connected to both D and G, so this is a correct answer. We are asked for the complete list, however, so we must continue to work through the answer choices. Choice (C) is Ms. Win. We can eliminate this choice immediately on the basis of it not including Ms. Petrucci. Choice (D) is Ms. Petrucci and Ms. Win. If we consult our diagram, indeed Ms. Win is connected to both D and G. Choice E adds Mr. Andrews to the list, but we have already eliminated him as a possible interpreter. Choice (D) is the correct answer.
Let’s try the second question.
Question Two
(2) Besides Ms. Win, who can converse with Ms. Farmer without an interpreter?
(A) Mr. Andrews and Ms. Petrucci
(B) Mr. Gaal and Mr. Das
(C) Mr. Gaal and Mr. Andrews
(D) Mr. Gaal and Ms. Petrucci
(E) Mr. Das and Ms. Petrucci
We are asked who can converse with Ms. Farmer without an interpreter. In the context of our network diagram, this question is asking to which other elements, other than W, is element F directly connected. By looking at our diagram, we see that F is connected to A, W, and G. Therefore the correct answer is choice (C), Mr. Gaal and Mr. Andrews (G and A on our diagram).
Question Three
(3) Which of the following pairs of people cannot converse without an interpreter?
(A) Mr. Andrews and Ms. Petrucci
(B) Mr. Das and Ms. Win
(C) Mr. Gaal and Ms. Petrucci
(D) Ms. Farmer and Mr. Das
(E) Mr. Andrews and Ms. Farmer
Starting with choice (A), we see that A and P are connected on our diagram, so this cannot be the correct answer. D and W are also connected, so we can eliminate choice (B). G and P are connected, so choice (C) is incorrect. Choice (D) seems to be the exception, as D and F are not connected on our diagram. To be sure, let’s check choice (E). We see that A and F are connected, so choice (D) represents the only pair of people (of the choices given) that cannot converse without an interpreter.
Let’s do one final question for this game, which is structurally different.
Question Four
(4) Of the five languages spoken by the six executives, which are the two most common?
(A) English and German
(B) English and Hindi
(C) French and Russian
(D) Russian and German
(E) Russian and English