Notification
You need to select an answer first.
So far we’ve dealt with if then statements that are categorical: No Great White Sharks are vegetarians.
Now we’re adding a level of complexity with some, all, and most. We’ll eventually visualize these relationships with Venn Diagrams.
This first video is beginner level and goes through the formal logic meanings of the following:
One way to visualize most, some, and or is to diagram them using overlapping circles (Venn Diagrams).
At Beverly Hills University (BHU), no students are on financial aid (FA).
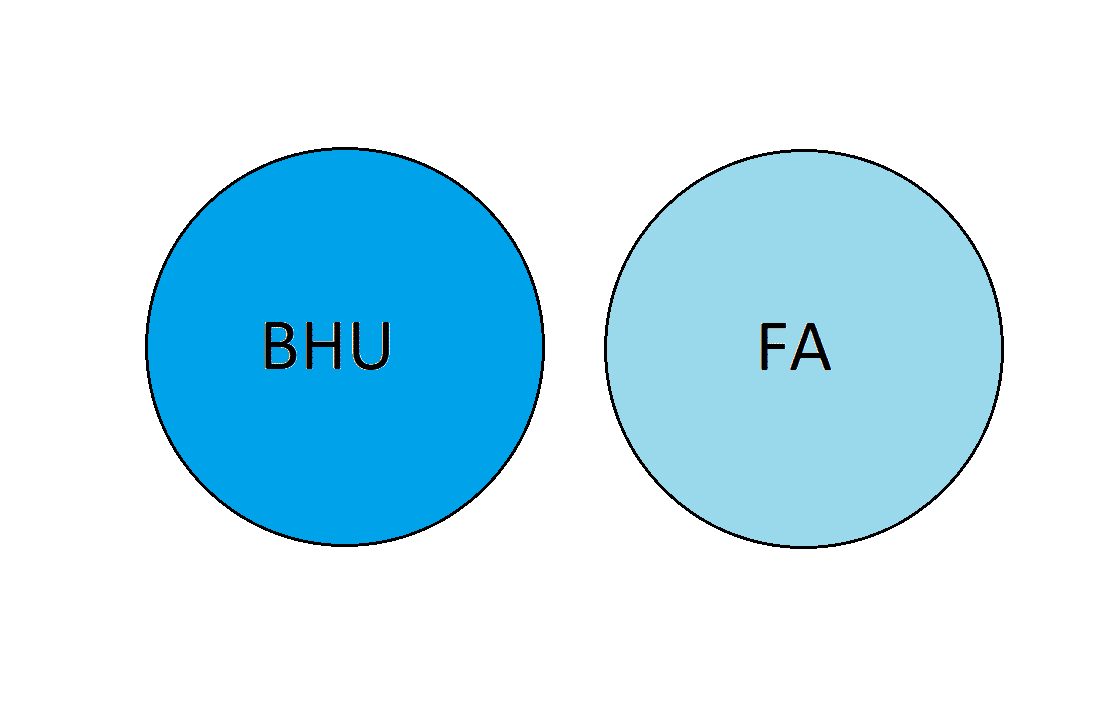
We can also understand the given statement as: if you are a student at Beverly Hills University, then you are not on financial aid. This means that the BHU and FA circles should not have any intersecting areas.
All grad students (GS) are higher-ed students (HES).
Some grad students (GS) are on financial aid (FA).
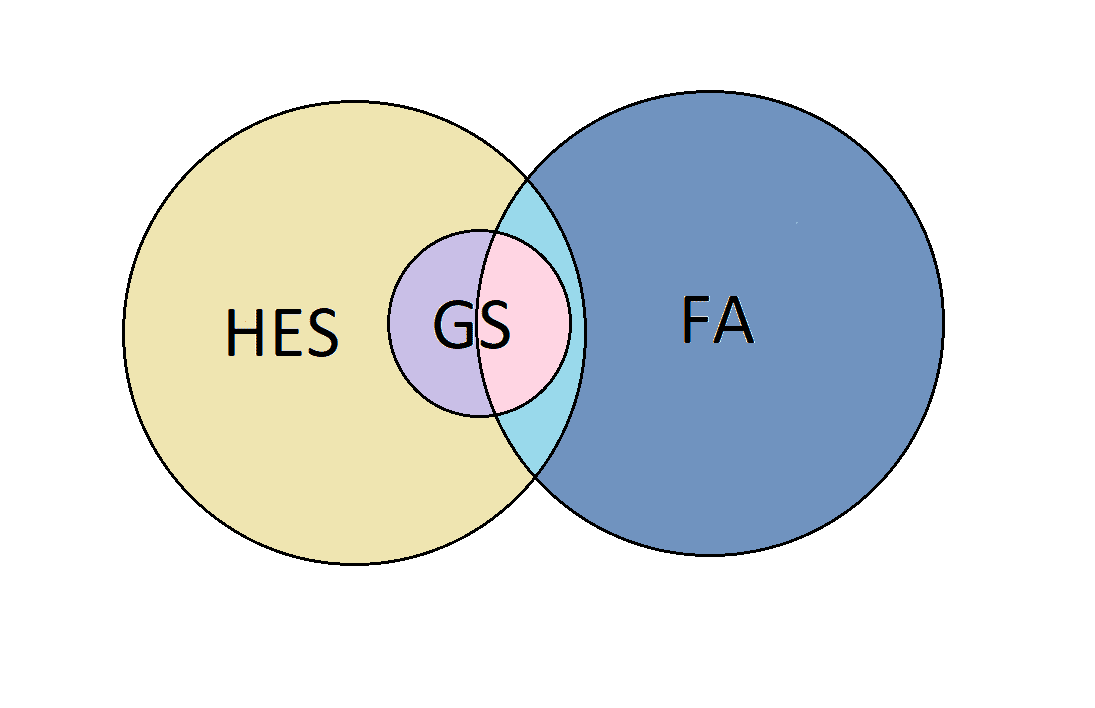
Given that all grad students are higher-ed students, the whole GS circle must be inside the HES circle. Moreover, since some grad students are on financial aid, then the GS and FA circles must have intersecting areas.
Next LSAT: Sep 08/ Sep 09
Premise 1: Most voters view Hillary unfavorably.
Premise 2: Most voters view Trump unfavorably.
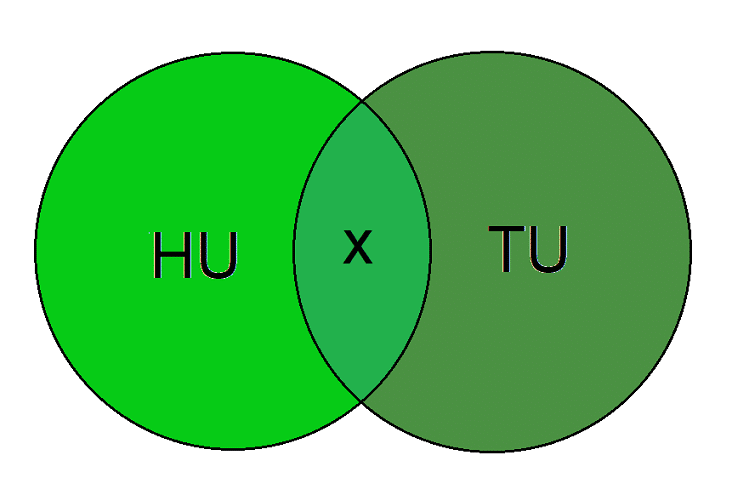
Since some voters view both Hillary Clinton and Donald Trump unfavorably, the circle representing the voters who view Hillary Clinton unfavorably should intersect with the circle representing the voters who view Donald Trump unfavorably.
The area with “x” represents the voters who view both Hillary Clinton and Donald Trump unfavorably, which is the inference that can be drawn.
All national scientists (S) are Ph.D. graduates (P), but not all Ph.D. graduates (P) are national scientists (S).
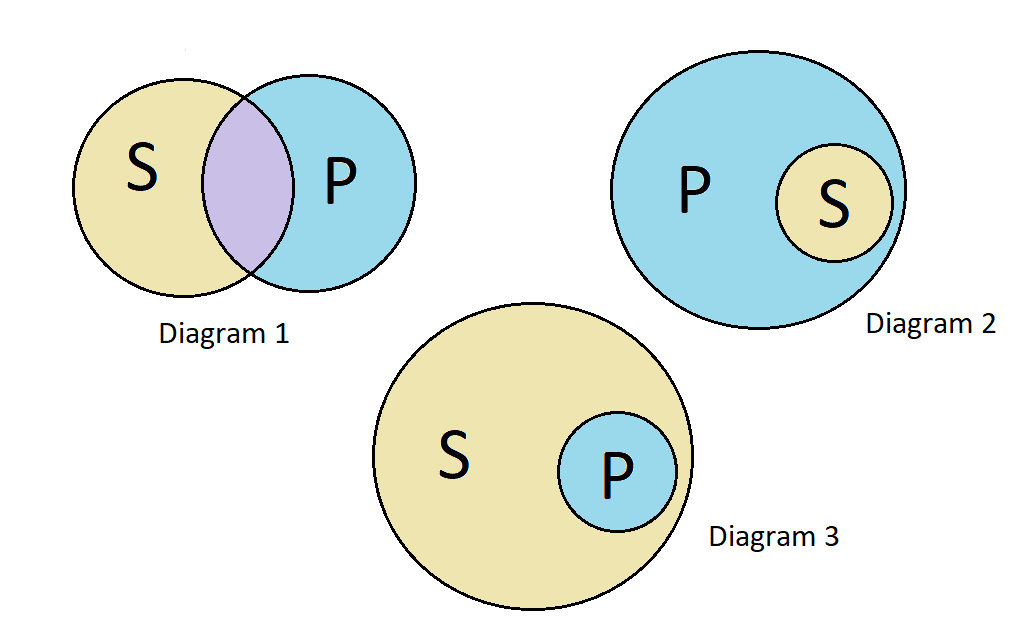
Diagram 2: The statement claims that if you are a national scientist (S), then you have to be a Ph.D. graduate (P). This means that the (S) circle should be inside the (P) circle because all (S) are (P). Therefore, the second diagram is the correct answer.
Diagram 1: Although this diagram meets the criterion that not all Ph.D. graduates (P) are national scientists (S), the whole (S) circle should be inside the (P) circle because the statement tells us that all (S) are (P). This diagram shows that some (S) are not (P), which is incorrect.
Diagram 3: This diagram does not show what the statement represents. The statement says that not all Ph.D. graduates (P) are national scientists (S). This means that the (P) circles should not be inside the (S) circle. Therefore, this is not the correct answer.
Some animals (A) are not reptiles (R), but all reptiles (R) are animals (A).
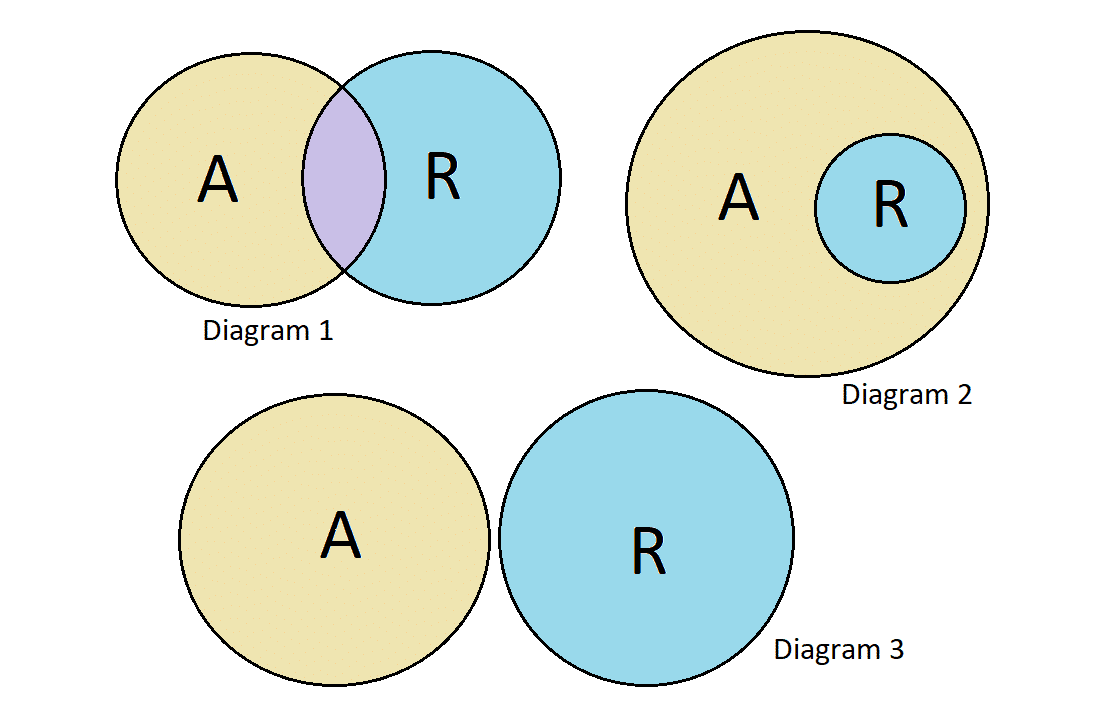
Diagram 2: The statement claims that there are animals that are not reptiles so the circle of animals (A) should have a part that does not intersect the circle of reptiles (R). Both the first and second diagrams meet this criterion, but the first one implies that there are reptiles that are not animals, which is wrong. The second best represents the statement that not all animals are reptiles because the whole (R) is inside (A), while not all (A) intersect (R).
Diagram 1: Although this diagram meets the criteria that circle (A) should have a part that does not intersect circle (R), it shows that there are (R) that are not part of (A). Therefore, it is incorrect.
Diagram 3: This diagram does not show any intersection between circle (A) and circle (R), but the statement shows that all (R) are (A) and thus, should have an intersection. This diagram presents that there is no intersection between (A) and (R), which is incorrect.
Some of the members of the organization (M) are foreigners (F).
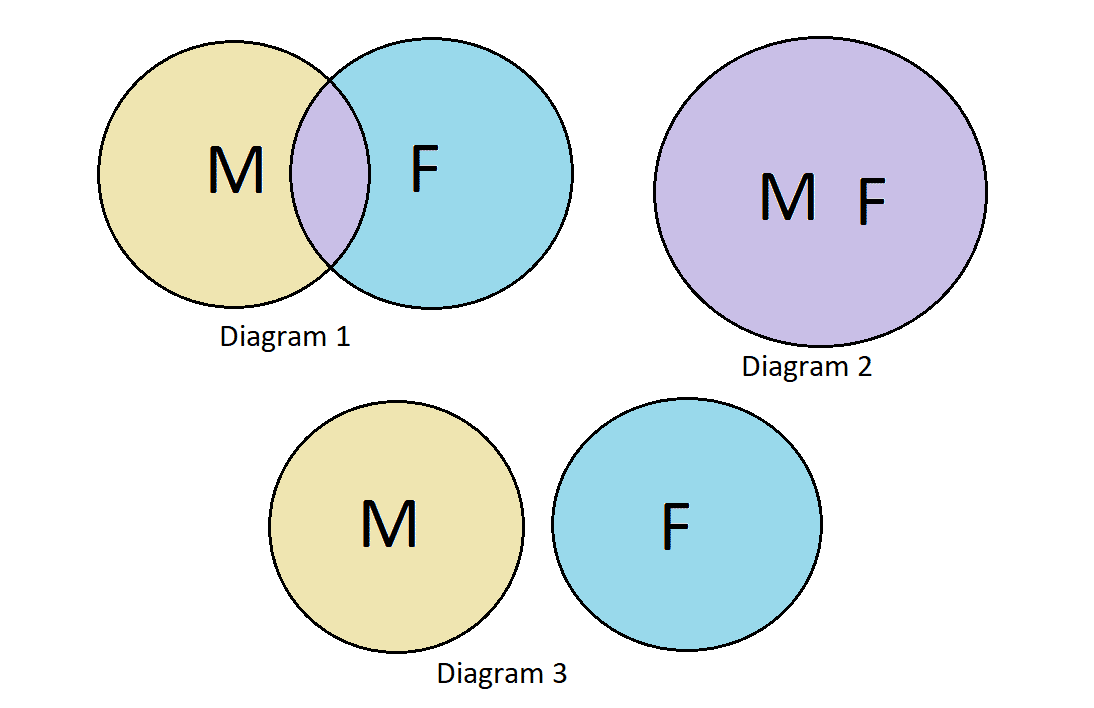
Diagram 1: The statement tells us some members of the organization (M) are foreigners (F). This means that there should be an intersection between the circle (M) and the circle (F). The first diagram shows exactly this relation, and it also shows that there are parts of (M) that are not part of (F) and there are parts of (F) that are not part of (M).
Diagram 2: This diagram shows the circle (M) and circle (F) are overlapping, which means that all (M) are (F), and all (F) are (M). However, the statement tells us that only some (M) are (F). Therefore, this is incorrect.
Diagram 3: This diagram shows that circle (M) and circle (F) have no intersection, but the statement claims that some (M) are (F), and thus, should have an intersection. Therefore, this is incorrect.
All businessmen (B) love money (M).
Some politicians (P) are businessmen (B).
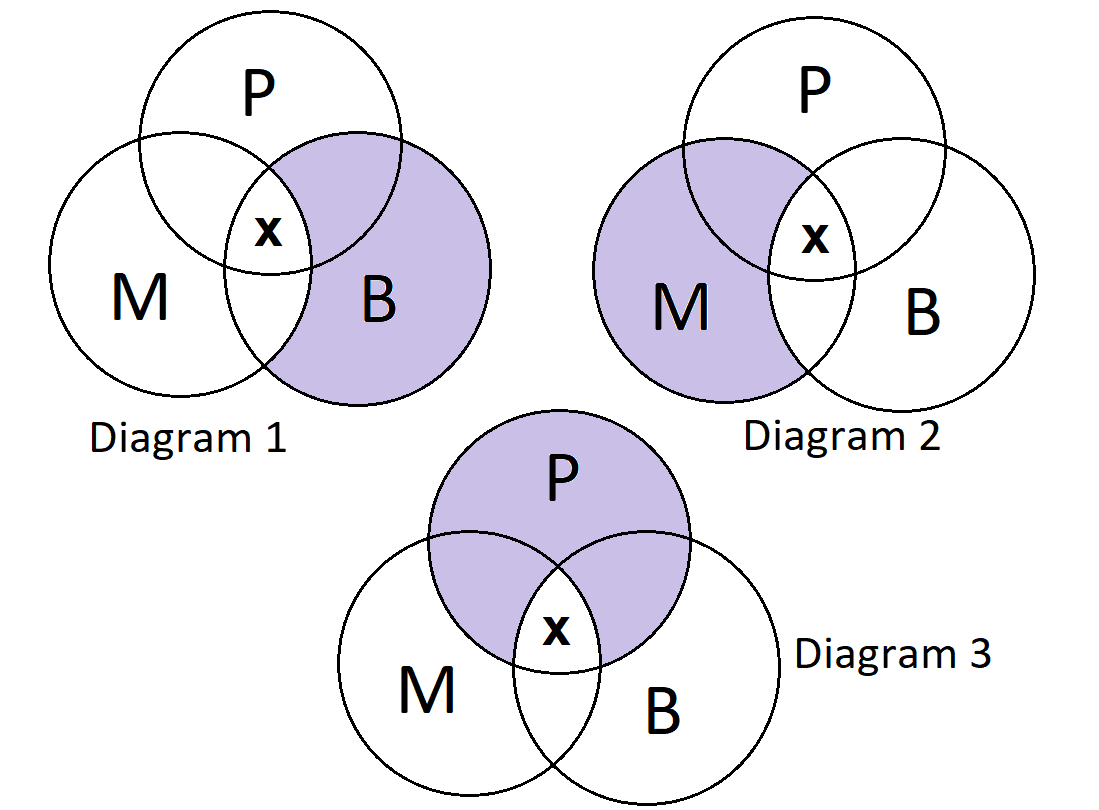
Diagram 1: The first statement claims that all (B) are (M), which means that parts of circle (B) that do not intersect circle (M) should be shaded. Moreover, the second statement states that some (P) are (B), which means that the “X” should be within the intersection of (P) and (B) that is not shaded. Hence, this is the correct answer.
Diagram 2: Although this diagram correctly presents the second statement, it is incorrect regarding the first statement. The shaded part should be where (B) does not intersect (M), but this diagram shows it the other way around. The parts of (M) that do not intersect (B) are shaded, which is the opposite.
Diagram 3: This diagram is simply incorrect because the shaded part does not represent the statements given in the question. The first statement claims that all (B) are (M), so the parts of circle (B) that do not intersect circle (M) should be the ones shaded and not parts of (P).
All who passed the Professional Exam (P) also passed the “logical reasoning” section of the exam (L).
Some people who passed the “reading comprehension” section (R) also passed the Professional Exam (P).
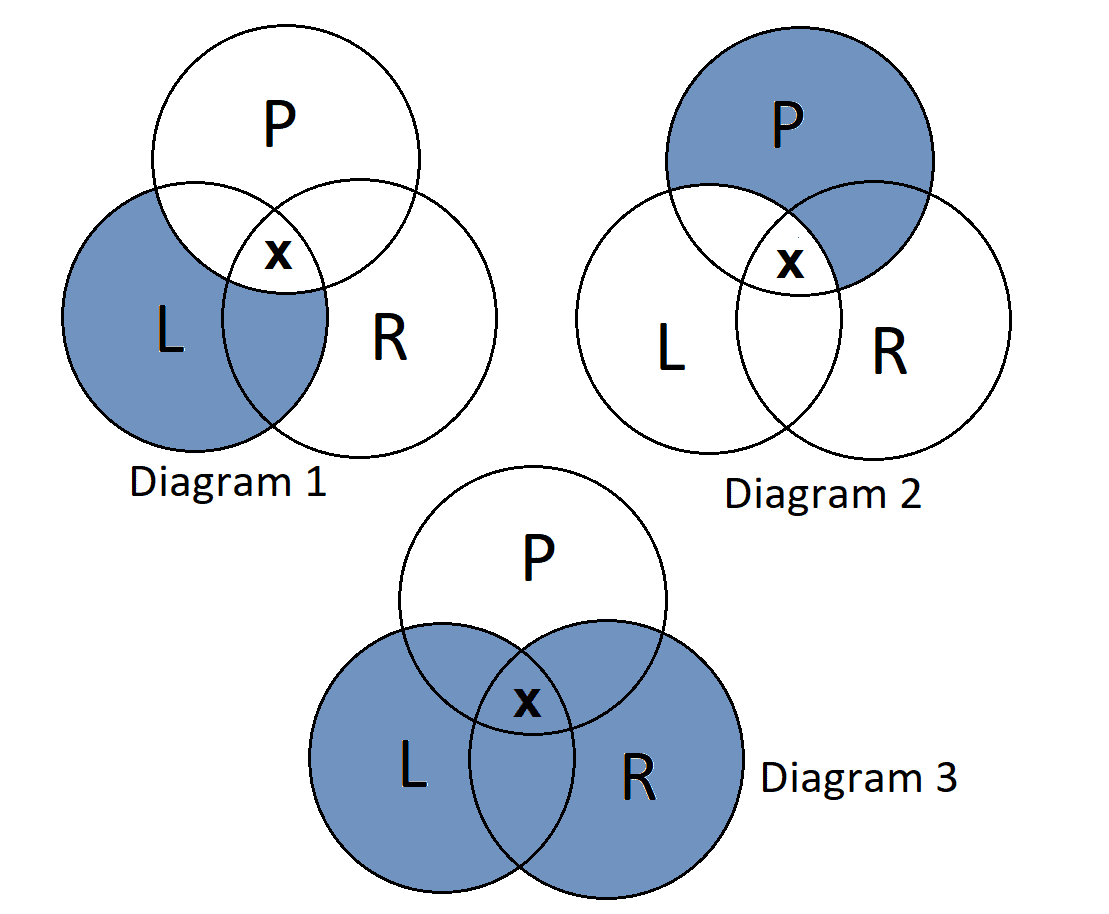
Diagram 2: The first statement presents that all (P) are (L) and thus, any (P) that does not intersect with (L) must be shaded. Furthermore, the second statement presents the intersection between circle (R) and circle (P). This means that “X” should be within the intersection of (R) and (P) that is not shaded.
Diagram 1: This diagram shades both the whole of circle (L) and circle (R). This is incorrect because it leaves only circle (P) remaining, and it presents relations that are far from what the statements represent.
Diagram 3: Although this diagram correctly shows the intersection of (R) and (P), the first statement presents that any (P) that does not intersect with (L) must be shaded. However, this diagram shows that (L) not intersecting with (P) is shaded, which is different from the meaning of the first statement. Therefore, this diagram is incorrect.
All of my college friends (F) will go to the party (P).
Some of my classmates in college (C) are also my friends (F).
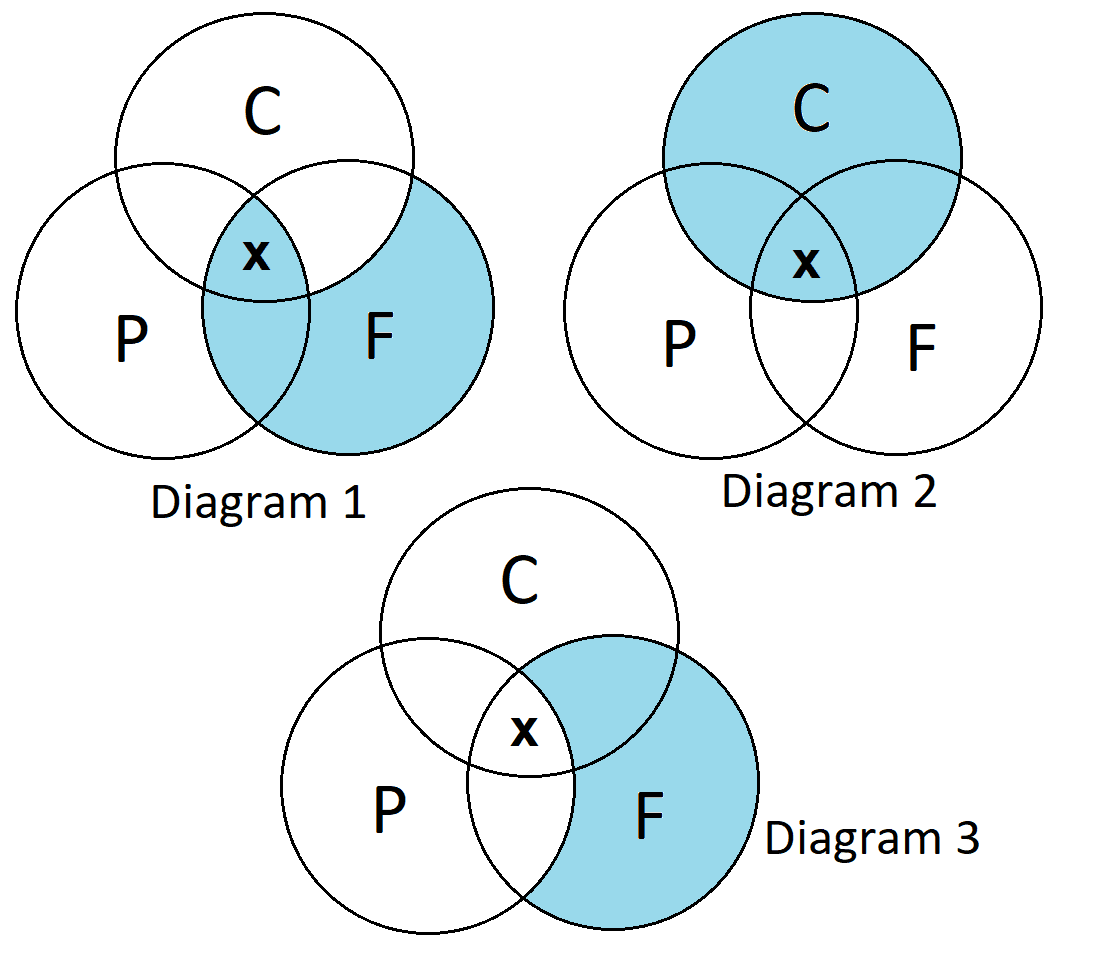
Diagram 2: The first statement presents that all (F) are (P). This means that parts of (F) that do not intersect with (P) should be shaded. Moreover, the second statement shows the intersection of (C) and (F). Therefore, the “X” should be within the part of the intersection of (C) and (F) that is not shaded.
Diagram 1: This diagram shows the whole circle (C) shaded, but the first statement states that all (F) are (P). This means that parts of (F) that intersect with (P) should not be shaded. Therefore, this diagram is incorrect.
Diagram 3: This diagram correctly shows the intersection of (C) and (F) as stated in the second statement. However, it incorrectly represents the first statement. The first statement shows that parts of (F) that do not intersect with (P) should be shaded, but this diagram shades the intersection of (F) and (P), which makes this diagram incorrect.
What if you take a contrapositive of the descriptive statements above? How do you describe the negation of all? The following video explains the logical significance of these terms:
You would think the opposite of all would be none, but it isn’t. The opposite of all (which you are going to be using often on the LSAT if you are taking the contrapositive of an all statement) is some are not.
All means 100% of something.

Some means greater than 0% (none) but not 100% (all).

Some are not means below 100% (all) down to 0% (none).

All dogs (D) are nice animals (NA).
The converse of “all” statements isn’t valid.
For example:
All dogs (D) are nice animals (NA).
All D → NA is not logically equivalent to NA → D (All nice animals are dogs).
NA → D is invalid.
All dogs (D) are nice animals (NA).
The negation of “all” is “some are not.”
The negation of “All dogs are nice animals” is not “No dogs are nice animals.” Its negation is “Some dogs are not nice animals.”
Note: The opposite of “nothing” is “some.”
Negations aren’t valid inferences.
“Life is a great adventure or nothing”
-Helen Keller
The contrapositive (show in red above) shows that the opposite of nothing is something (the opposite of nothing isn’t everything).
All LSATs (L) are hard tests (HT).
All L → HT
1. Some tests that are not hard are not an LSAT.
Some ~HT → ~L
This is a valid inference because this is precisely the contrapositive of the original statement. A statement and its contrapositive are logically equivalent.
2. All hard tests are LSAT tests.
ALL HT → L
This is an invalid inference because this is the converse of the original statement. A converse is not equivalent to the original statement.
3. Some LSATs are not hard.
Some L → ~HT
This is an invalid inference because it directly contradicts the original statement.
All licensed engineers (LE) passed the professional engineering exam (P).
All LE → P
1. All people who passed the professional engineering exam are licensed engineers.
All P → LE
This is an invalid inference because this is the converse of the original statement. A statement and its converse are not logically equivalent.
2. Some people who did not pass the professional engineering exam are not licensed engineers.
Some ~P → ~LE
This is a valid inference because it is the contrapositive of the original statement. The contrapositive of a statement is logically equivalent to the statement itself.
3. Some licensed engineers did not pass the professional engineering exam.
Some LE → ~P
This is an invalid inference because it directly contradicts the original statement.
This can be a confusing question, but all it’s really asking you to do is use substitution (athletes for bankers).
The three dots symbolize the conclusion.
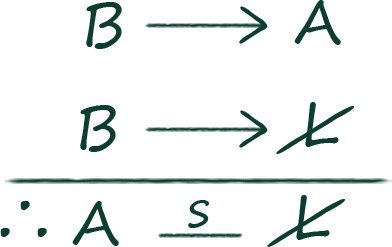
This is an adaptive drill: The questions will get harder or easier depending on your performance. You can't go backwards or change prior answers.
Complete: 0 / 3 correct
Next LSAT: Sep 08/ Sep 09